Z3 SMT Solver
Z3 הינו SMT Solver אשר נכתב על ידי Microsoft:
https://github.com/Z3Prover/z3
באופן אישי יצא לי להשתמש ב-Z3 במספר אתגרים שונים. כאשר עליכם למצוא סיסמא עבור שם משתמש כלשהו והלוגיקה היא לוגיקה מתמטית, Z3 יעזור לכם למצוא את הסיסמא
להלן סרטון המדגים כיצד לבצע את התהליך:
Solver הוא סוג של הרחבה ל-SAT Solver (satisfiability), SAT Solver מקבל סט של תנאים והוא בודק האם הם מחזירים True או False. במידה וכל התנאים מחזירים True סימן שיש לנו פתרון לתנאים שהתקבלו.
SAT עובד רק עם תנאים שהם בוליאניים, SMT עושה את אותו הדבר עבור כל סוגי התנאים כך שאפשר לכתוב תרגיל מתמטי רגיל או להכניס לו בעיה כלשהי שאנחנו רוצים שיפתור עבורנו.
לדוגמה:
(x > 1 OR y < 5) AND
(x = 2 OR x = 3 and x = y) AND
(y > 0 OR x>y)
התוכנה שלנו תבדוק את כל התנאים ותגיע לפתרון, היא תיקח בשורה הראשונה את x > 1 ואז בשורה השנייה את
x = 3 and x = y ובשורה השלישית את y > 0 הכל מסתדר אז התשובה היא True.
אך במידה והיינו מקבלים משהו כזה:
( x > 2*x, x > 0 )
נקבל unsat מכיוון שלא ניתן לפתור את התרגיל, לכן כשנעבוד עם z3, תחילה נבדוק האם התרגיל פתיר באמצעות הפקודה check() ורק לאחר מכן אנחנו נפתור אותו באמצעות ()model מה שנראה כך:
If solv.check() == sat:
solv.model()
כדי להתקין z3 אנו נשתמש בפקודה הבאה:
pip install z3-solver
ב-z3 תחילה עלינו להגדיר את המשתנים שלנו באמצעות Int, BitVec, Bool או כל דבר אחר בהתאם לתרגיל, לדוגמה אם נרצה לפתור את התרגיל הבא בקלות ללא ביצוע בדיקה:
x = Int('x')
y = Int('y')
solve(x > 2, y < 10, x + 2*y == 7)
כך בעצם הגדרנו את x ו-y שהם מספרים שעונים על התרגיל המתמטי שמכניסים ל-solve והתוצאה היא:
[y = 0, x = 7]
כמו כן ניתן לפשט תרגיל מתמטי על ידי הפקודה simplify כך:
x = Int('x')
y = Int('y')
print simplify(x + y + 2*x + 4)
התוצאה תהיה פישוט התרגיל המתמטי:
4 + 3*x + y
כאשר מגדירים תרגיל מתמטי אפשר לשמור אותו במשתנה ואז אפשר יהיה לעבוד איתו בצורה הבאה:
x = Int('x')
y = Int('y')
n = x + y >= 3
print n
print "num args: ", n.num_args()
print "children: ", n.children()
print "1st child:", n.arg(0)
print "2nd child:", n.arg(1)
print "operator: ", n.decl()
print "op name: ", n.decl().name()
התוצאה תראה כך:
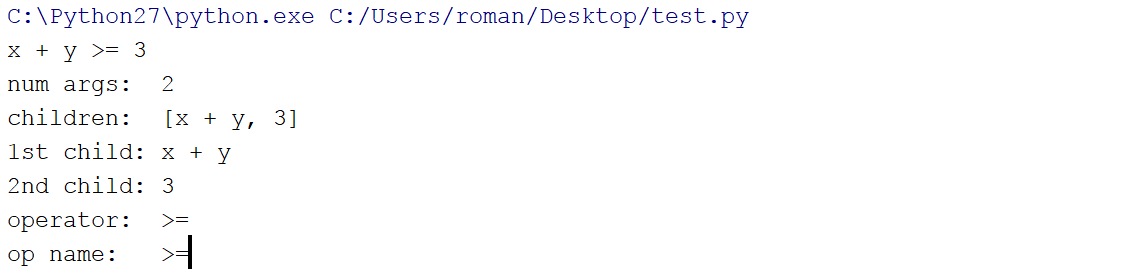
אם נרצה שהתוצאה תהיה במספרים ממשיים (שברים), נשתמש ב-Real:
x = Real('x')
y = Real('y')
solve(x**2 + y**2 == 3, x**3 == 2)
set_option(precision=30)
print "Solving, and displaying result with 30 decimal places"
solve(x**2 + y**2 == 3, x**3 == 2)
התוצאה:

השתמשנו כאן בפקודה:
set_option(precision=30)
כך אנחנו מגדירים בעצם כמה ספרות אנחנו רוצים אחרי הנקודה, הרעיון מאחורי set_option הוא בעצם הגדרה של הסביבה של z3.
במידה ויש משתנה שהוא True או False אנו נגדיר אותו כך:
p = Bool('p')
q = Bool('q')
r = Bool('r')
solve(r == Not(q), Or(Not(p), r))
והתוצאה תראה כך:
[q = True, p = False, r = False]
אם ניקח תרגיל מתמטי כלשהו כפי שראיתם בסרטון וננסה לפתור אותו:
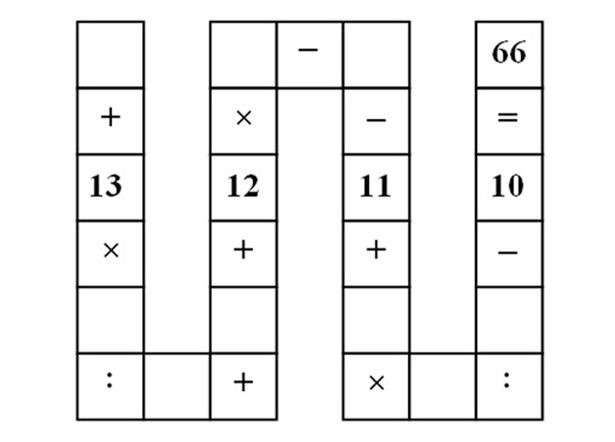
יהיה עלינו בסה"כ להגדיר את כל המשתנים שלנו ואת תנאי התרגיל בצורה הבאה, תחילה נגדיר את כל המשתנים שלנו:
from z3 import *
x1 = Int("x1")
x2 = Int("x2")
x3 = Int("x3")
x4 = Int("x4")
x5 = Int("x5")
x6 = Int("x6")
x7 = Int("x7")
x8 = Int("x8")
x9 = Int("x9")
לאחר מכן נגדיר solver כדי שנוכל להכניס לתוכו את התנאי שלנו ולבחון אותו:
solv = Solver()
solv.add(x1+13*x2/x3+x4+12*x5-x6-11+x7*x8/x9-10 == 66)
solv.add(x1 > 0, x2 >0 ,x3 >0 ,x4 > 0,x5 >0 ,x6>0,x7>0,x8>8,x9>0)
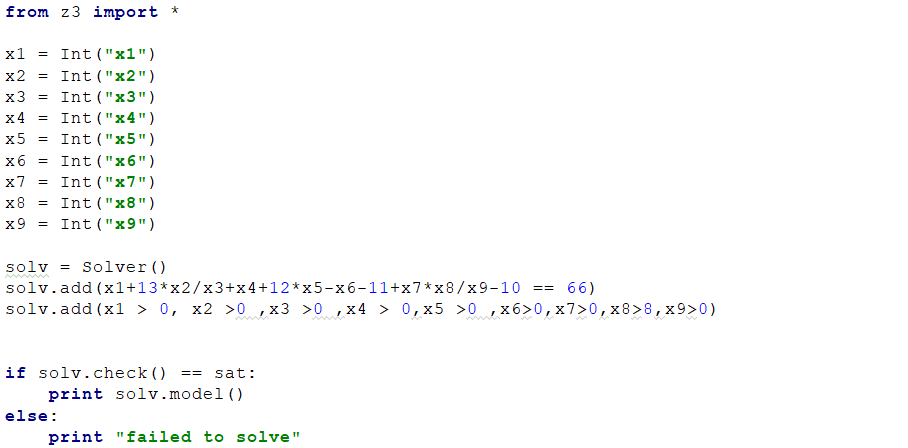
לסיום נבדוק האם התרגיל פתיר באמצעות SAT Solver ונבקש מ-z3 לפתור את התרגיל על ידי שימוש בmodel-:
if solv.check() == sat:
print solv.model()
else:
print "failed to solve"
התוצאה תראה כך:
במאמר הבא אציג לכם כיצד ניתן לפתור סודוקו באמצעות z3 ואף נפתור תרגיל הנדסה לאחרו אשר מצריך מאיתנו להבין מה הסיסמא באמצעות z3, שווה לחכות!

